Trong bài này chúng ta sẽ tìm hiểu một số độ đo có thể đánh giá được sự khác biệt giữa hai phân bố xác suất.

Cross entropy

Với hai phân bố xác suất rời rạc $\mathbf{p} = (p_1, p_2, \dots, p_n)$ và $\mathbf{q} = (q_1, q_2, \dots, q_n)$. Cross entropy của hai phân bố xác suất được định nghĩa như sau:

\[H(\mathbf{p},\mathbf{q}) = - \sum_{i=1}^{n}p_{i} \log q_{i}\]

trong đó $n$ là số lượng classes cần phân loại.

Cross entropy giúp đo lường độ tương quan giữa hai phân bố xác suất. Đối với các bài toán phân loại chúng ta có $\sum_{i=1}^{n} p_i = \sum_{i=1}^{n} q_i = 1$.

Một số tính chất của cross entropy:

• $H(\mathbf{p},\mathbf{q}) \geq H(\mathbf{p})$, với $H(\mathbf{p}) = - \sum_{i=1}^{n}p_{i} \log p_{i}$ - entropy đo lường giá trị trung bình của $logp(x)$ theo phân phối $p(x)$. Có thể chứng minh bất đẳng thức này với Gibb;s inequality, log sum inequality, Jensen’s inequality. Dấu bằng xảy ra khi $p_i = q_i, \forall i=\overline{1, n}$.
• $H(\mathbf{p},\mathbf{q}) \neq H(\mathbf{q},\mathbf{p})$ hay cross entropy không có tính đối xứng.
• Trong các bài toán phân loại, $H(\mathbf{p},\mathbf{q})$ được sử dụng như hàm mất mát với $\mathbf{p}$ là phân bố biết trước, $\mathbf{q}$ là phân bố cần dự đoán. Chúng ta cần đi cực tiểu hóa hàm $H(\mathbf{p},\mathbf{q})$ để tối ưu mô hình, nghĩa là đi làm cho hai phân phối $\mathbf{p}$ và $\mathbf{q}$ tương quan với nhau.

Chúng ta đi giải quyết bài toán cực tiểu của $H(\mathbf{p},\mathbf{q})$ với phân bố $\mathbf{p}$ cho trước (cố định).

\[\mathbf{q}^* = \underset{\mathbf{q}}{\text{argmin}} H(\mathbf{p},\mathbf{q}) = \underset{\mathbf{q}}{\text{argmin}} -\sum_{i=1}^{n}p_{i} \log q_{i}\]

trong đó $\sum_{i=1}^{n} p_i = \sum_{i=1}^{n} q_i = 1$. Đây là bài toán tối ưu lỗi với điều kiện ràng buộc, cách đơn giản chúng ta đưa về hàm Langrange.

\[L(\mathbf{p},\mathbf{q}, \lambda) = -\sum_{i=1}^{n}p_i\log({q_i}) + \lambda (\sum_{i=1}^{n} q_i - 1)\]

Chú ý: Ở đây ghi cost function phụ thuộc vào phân bố cho trước $\mathbf{p}$ nhưng phải nhớ phân bố đó đã biết.

Chúng ta đi tính đạo hàm bậc một theo $q_i$ và $\lambda$:

\[\left\{ \begin{matrix} \nabla_{q_i} L(\mathbf{p}, \mathbf{q}, \lambda) &=& - {\frac{p_i}{q_i}} + \lambda~~~ &, \forall i=\overline{1, n} ~~~ \\ \nabla_{\lambda} L(\mathbf{p}, \mathbf{q}, \lambda) &=& \sum_{i=1}^{n} q_i - 1 & ~~~ \end{matrix} \right.\]

Tại các điểm cực trị chúng ta có $\frac{p_1}{q_1} = \frac{p_2}{q_2} = \dots = \frac{p_C}{q_C} = \lambda$, điều này đồng nghĩa với việc hai phân bố $\mathbf{p}$ và $\mathbf{q}$ tương đồng nhau.

Mặt khác $\nabla_{q_i}^2 L(\mathbf{p}, \mathbf{q}, \lambda) = \frac{p_i}{q_i^2} \geq 0, \forall i=\overline{1, n}$ nên cost function là một hàm lồi (nhớ đến parabol cho dễ hình dung). Do vậy $\mathbf{q} = \mathbf{p}$ chính là điểm cực tiểu, điểm cực tiểu này làm cho phân bố dự đoán sát với phân bố thực tế nhất.

Kullback Leibler divergence

Ngoài cross entropy còn có một số độ đo khác để xác định khác biệt giữa hai phân bố như Kullback leiber divergence - nếu 2 phân bố trùng nhau nó sẽ trả về 0.

Đối với 2 phân bố rời rạc $p(x), q(x)$ ta có:

\[D_{\text{KL}}(p||q) = \sum_{i=1}^n p(x_i)log \left ( \frac{p(x_i)}{q(x_i)} \right ) = -\sum_{i=1}^{n}p(x_i) \log q(x_i) + \sum_{i=1}^{n}p(x_i) \log p(x_i) = H(p,q) - H(p)\]

Quy ước:

• $q(x) = 0$, $p(x)$ hữu hạn thì coi $\text{log} q(x)\rightarrow - \infty $, do đó $D_{KL}(p | q) = + \infty$.
• $p(x) = 0$ thì coi $p(x) \text{log}p(x) = 0$, không có đóng góp gì vào $D_{KL}(p | q) = + \infty$

Nếu hai phân phối liên tục chúng ta có:

\[D_{KL}(p \| q) = \int_{\chi} p(x) \log \frac{p(x)}{q(x)} dx\]

trong đó ${\chi}$ là miền xác định của $x$.

Chú ý: Ở đây ghi $p(x)$, nếu phân bố rời rạc hiểu đó à xác suất là $x$, nếu là phân bố liên tục thì hiểu đó là hàm mật độ xác suất (density probability function).

Chúng ta đi tìm cực tiểu của $D_{KL}(p | q)$.

$p = (p_1, p_2, \dots, p_n)$, $q = (q_1, q_2, \dots, q_n)$. Nếu $q_i = 0$ theo quy ước trên chúng ta có $D_{KL}(p | q) = + \infty$.

Xét hàm số $f(x) = -\text{log}(x), ~~ x > 0$ (trường hợp bằng 0 vừa xét ở trên). Ta có:

\[\nabla_x^2{f(x)} = \frac{1}{x^2} > 0\]

Do đó $f(x)$ là một hàm lồi ngặt trên miền $x \in (0, 1]$ (khoảng xác suất mình đang xét). Vì vậy nó thỏa mãn bất đẳng thức Jensen với hàm lồi:

\[\lambda f(x_1) + (1-\lambda) f(x_2) \geq f(\lambda x_1 + (1-\lambda) x_2), ~~~ \forall \lambda \in (0, 1]\]

Tổng quát ta sẽ có:

\[\sum_{i=1}^{n}\lambda_i f(x_i) \geq f(\sum_{i=1}^{n}\lambda_i x_i)\]

trong đó $\sum_{i=1}^{n} \lambda_i = 1$, $\lambda_i \in (0, 1] ~~ \forall i = \overline{1, n}$.

Áp dụng bắt đẳng thức Jensen ta có:

\[\begin{align*} D_{\text{KL}}(p||q) = \sum_{i=1}^n p_i log \left ( \frac{p_i}{q_i} \right ) &= \sum_{i=1}^n p_i log \left ( \frac{q_i}{p_i} \right ) \\ &= \sum_{i=1}^n p_i f \left ( \frac{q_i}{p_i} \right ) \geq f \left ( \sum_{i=1}^{n}p_i \frac{q_i}{p_i} \right ) = log(1) = 0 ~~ \forall x \in (0, 1] \end{align*}\]

Kết hợp 2 trường hợp ta có $D_{\text{KL}}(p | q)$ có giá trị nhỏ nhất bằng 0 với $x \in (0, 1]$. Dấu = xảy ra khi:

\[\frac{q_1}{p_1} = \frac{q_2}{p_2} = \dots = \frac{q_n}{p_n} = \lambda\]

Điều này đồng nghĩa với việc phân phối $p(x)$ và $q(x)$ đồng nhất nhất. Như ở trên chúng ta có $D_{\text{KL}}(p | q) = H(p, q) - H(p)$, do đó dễ dàng suy ra $H(p, q) \geq H(p)$.

Tích chất của Kullback Leibler divergence:

• Không bị chặn
• Không có tính chất dối xứng

Jensen–Shannon Divergence

Jensen–Shannon Divergence cũng là độ đo sự khác biệt giữa hai phân bố, nó có tính đối xứng và bị chặn.

\[D_{JS}(p \| q) = \frac{1}{2} D_{KL}(p \| \frac{p + q}{2}) + \frac{1}{2} D_{KL}(q \| \frac{p + q}{2})\]

Ở đây $\frac{p+q}{2}$ là phân phối trung bình của hai phân phối $p$ và $q$. Chúng ta đo khoảng cách giữa 2 phân bố $p$, $q$ thông qua khoảng cách giữa hai phân bố $p$, $\frac{p+q}{2}$ và hai phân bố $q$, $\frac{p+q}{2}$.

\[\begin{align*} D_{JS}(p \| q) &= \frac{1}{2} D_{KL}(p \| \frac{p + q}{2}) + \frac{1}{2} D_{KL}(q \| \frac{p + q}{2}) \\ &= \frac{1}{2} \sum_{i=1}^{n}p_i \text{log}p_i - \frac{1}{2} \sum_{i=1}^{n}p_i \text{log}(\frac{p_i + q_i}{2}) + \frac{1}{2} \sum_{i=1}^{n}q_i \text{log}q_i - \frac{1}{2} \sum_{i=1}^{n}q_i \text{log}(\frac{p_i + q_i}{2}) \\ &= -\sum_{i=1}^{n}(\frac{p_i + q_i}{2})\text{log}(\frac{p_i + q_i}{2}) + \frac{1}{2} \sum_{i=1}^{n}p_i \text{log}p_i + \frac{1}{2} \sum_{i=1}^{n}q_i \text{log}q_i \\ &= H(\frac{p+q}{2}) - \frac{1}{2}H(p) - \frac{1}{2}H(q) \end{align*}\]

Đối với Kullback Leibler divergence khi $q(x)$ tiến gần đến 0 và $p(x)$ hữu hạn thì $D_{KL}(p | q)$ sẽ tiến đến $+ \infty$. Tuy nhiên đối với Jensen–Shannon Divergence ta có:

\[D_{KL}(p \| \frac{p+q}{2}) = p\log(\frac{2p}{p+q}) \leq p \text{log}2\]

Trường hợp $p=0$ đã xét riêng rồi $D_{KL}(p | \frac{p+q}{2}) = 0$ vì coi $\lim_{x \to 0}x \text{log}x = 0$. Điều này có nghĩa rằng Jensen–Shannon Divergence có giá trị hữu hạn và thích hợp hơn Kullback Leibler divergence trong việc xác định khoảng cách giữa hai phân phối.

Hội tụ của GANs và hội tụ của Jensen–Shannon Divergence

\[\begin{aligned} \min_G \max_D L(D, G) & = \mathbb{E}_{x \sim p_{r}(x)} [\log D(x)] + \mathbb{E}_{z \sim p_z(z)} [\log(1 - D(G(z)))] \\ & = \mathbb{E}_{x \sim p_{r}(x)} [\log D(x)] + \mathbb{E}_{x \sim p_g(x)} [\log(1 - D(x)] \end{aligned}\]

Ở đây:

• $p_z$ - phân bố của input noise $z$ thường là normal distribution
• $p_g$ - phân bố của dữ liệu generator tạo ra
• $p_r$ - phân bố của dữ liệu thật

Chú ý: Trong công thức trên chúng đã đã bỏ đi dấu “-“ nên min max bị đảo ngược.

Chúng ta sẽ đi tìm giá trị tối ưu của D hàm sau đạt max để:

\[L(G, D) = \int_x \bigg( p_{r}(x) \log(D(x)) + p_g (x) \log(1 - D(x)) \bigg) dx\]

Đặt $\tilde{x} = D(x), A=p_{r}(x), B=p_g(x)$. Chúng ta có thể bỏ qua dấu tích ohaan vởi $x$ được lấy trên tất cả giá trị có thể. Phân bên trong dấu tích phân là:

\[\begin{aligned} f(\tilde{x}) & = A log\tilde{x} + B log(1-\tilde{x}) \\ \frac{d f(\tilde{x})}{d \tilde{x}} & = A \frac{1}{ln10} \frac{1}{\tilde{x}} - B \frac{1}{ln10} \frac{1}{1 - \tilde{x}} \\ & = \frac{1}{ln10} (\frac{A}{\tilde{x}} - \frac{B}{1-\tilde{x}}) \\ & = \frac{1}{ln10} \frac{A - (A + B)\tilde{x}}{\tilde{x} (1 - \tilde{x})} \\ \end{aligned}\]

Cho đạo hàm bậc một $\frac{d f(\tilde{x})}{d \tilde{x}} = 0$ chúng ta nhận được giá trị tốt nhất cho discriminator:

\[D^*(x) = \tilde{x}^* = \frac{A}{A + B} = \frac{p_{r}(x)}{p_{r}(x) + p_g(x)} \in [0, 1]\]

Đạo hàm bậc hai của $f(\tilde{x}) < 0$ nên $D^*(x)$ nhận được ở trên chính là điểm cực đại.

\[\begin{align*} L(G, D^*) & = \int_x p_r(x) \log \bigg( \frac{p_r(x)}{p_r(x) + p_g(x)} \bigg) + p_g(x) \log \bigg( \frac{p_g(x)}{p_r(x) + p_g(x)} \bigg) dx \\ & = \int_x p_r(x) \log \bigg( \frac{2~p_r(x)}{p_r(x) + p_g(x)} \bigg) + p_g(x) \log \bigg( \frac{2~p_g(x)}{p_r(x) + p_g(x)} \bigg) dx - \log(2) \int_x p_r(x) - \log(2) \int_x p_g(x) dx \\ & = D_{KL}(p_r(x) \Vert \frac{p_g(x)+p_r(x)}{2}) + D_{KL}(p_g(x) \Vert \frac{p_g(x)+p_r(x)}{2}) - 2\log2 \\ & = 2D_{JS}(p_r(x) \Vert p_g(x)) - 2\log2 \end{align*}\]

\(G^*\) mà tối ưu nhất sẽ cho \(p_g(x)\) trùng với \(p_r(x)\) thì khoảng cách Jensen-Johnson \(D_{JS}(p_r(x) \parallel p_g(x)) = 0\) và khi đó \(L(G, D^*) = -2\log2\) như chúng ta sẽ nhận được ở bên dưới.

Global optimal

GAN hội tụ khi chúng ta có $p_g = p_r$ (phân phối của ảnh thật và ảnh tạo ra từ generator tương đồng nhau) và $D^*(x) = \frac{1}{2}$ (thay vào phương trình trên).

\[\begin{aligned} L(G, D^*) &= \int_x \bigg( p_{r}(x) \log(D^*(x)) + p_g (x) \log(1 - D^*(x)) \bigg) dx \\ &= \log \frac{1}{2} \int_x p_{r}(x) dx + \log \frac{1}{2} \int_x p_g(x) dx \\ &= -2\log2 \end{aligned}\]

Độ đo Earth-Mover (EM) hoặc Wasserstein

$p_r$ là phân phối của dữ liệu thật, $p_g$ là phân phối của dữ liệu sinh, sinh ra từ generator. Wasserstein là giá trị cận dưới (infimum) của khoảng cách giữa phép dịch chuyển $p_r$ sang $p_g$ theo công thức sau:

\[W(p_r, p_g) = \inf_{\gamma \sim \Pi(p_r, p_g)} \mathbb{E}_{(x, y) \sim \gamma}[\| x-y \|]\]

$\Pi(p_r, p_g)$ là phân phối đồng thời (joint probability distribution) của hai phân phối $p_r$ và $p_g$. $p_r$ và $p_g$ là phân phối biên (margin distribution). $\gamma(x, y)$ là giá trị của phân phối đồng thời của $(x, y)$, ta có $\sum_{x} \gamma(x, y) = p_g(y)$ và $\sum_{y} \gamma(x, y) = p_r(x)$. Khonagr cách Wasserstein là cận dưới lớn nhất của kỳ vọng khoảng cách giữa hai điểm $(x, y)$ theo phân phối $\gamma (x, y)$ (khoảng cách được xác định them norm l2).

Khoảng cách Wassersteiin như GAN loss function

Rất khó để sử dụng hết các joint distributions $\Pi(p_r, p_g)$ để tính $\inf_{\gamma \sim \Pi(p_r, p_g)}$. Để đơn giản hơn chúng ta sẽ chuyển về bài toán đối ngẫu Kantorovich-Rubinstein:

\[W(p_r, p_g) = \frac{1}{K} \sup_{\| f \|_L \leq K} \mathbb{E}_{x \sim p_r}[f(x)] - \mathbb{E}_{x \sim p_g}[f(x)]\]

trong đó $sup$ (supremum) đối lập với $inf$ (infimum), ở đây chúng ta muốn lấy cận trên lớn nhất, đơn giản thì lấy giá trị max.

Lipschitz continuity

Hàm số f trong dạng mới của Wasserstein metric cần thỏa mãn $| f |_L \leq K$ hay hàm $f$ cần K-Lipschitz continuous. Khoảng cách Wasserstein chính là supremum (cận trên nhỏ nhất) của chênh lệch kỳ vọng giữa phân phối của dữ liệu thật và dữ liệu sinh được đo lường thông qua hàm $f(x)$.

Hàm số $f: \mathbb{R} \rightarrow \mathbb{R}$ được gọi là K-Lipschitz continuous nếu tông tại hằng số $K \geq 0$ sao cho với tất cả $x_1, x_2 \in \mathbb{R}$ ta có:

\[|f(x_1) - f(x_2)| \leq K |x_1 - x_2|\]

\(K\) - hằng số Lipschitz cho hàm \(f\). Hàm số khả vi, liên tục trên toàn miên xác định thì liên tục Lipschitz, bởi vì đạo hàm được ước lượng thông qua \(\frac{\lvert f(x_1) - f(x_2) \rvert}{\lvert x_1 - x_2 \rvert}\) bị chặn. Tuy nhiên hàm số liên tục Lipschitz chưa chắc đã khả vi trên toàn miền, ví dụ \(f(x) = \lvert x \rvert\).

Như vậy để áp dụng Wasserstein GAN, chúng ta chỉ cần tìm hàm liên tục 1-lipschitz. Kiến trúc mạng của discriminator sẽ được giữ nguyên và chúng ta chỉ bỏ qua hàm sigmoid ở cuối. Như vậy hàm dự báo output chính là một linear projection và đó là một hàm liên tục 1-lipchitz. Kết quả dự báo sau cùng sẽ đưa ra một điểm số scalar thay vì xác suất. Điểm này có thể được hiểu là điểm đánh giá chất lượng hình ảnh được sinh ra theo mức độ giống với ảnh thật. Tính chất của discriminator đã thay đổi từ phân loại ảnh reak/fake sang chấm điểm chất lượng ảnh nên để phù hợp với mục tiêu thì chúng ta thay đổi tên của discriminator thành critic.

Để hiểu rõ hơn sự khác biệt giữa kiến trúc GAN và WGAN chúng ta cùng theo dõi hình bên dưới:

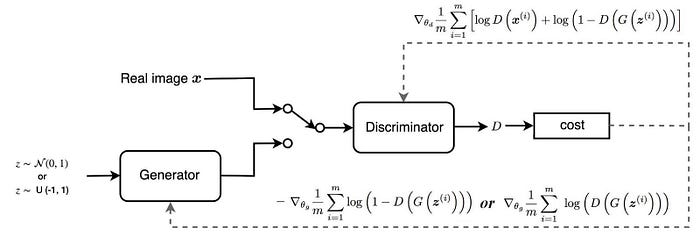
Tổng kết lại ta có sự khác biệt giữa GAN và WGAN đó là :

• Bỏ hàm sigmoid ở critic model và thay vào đó là linear projection.
• Ở model GAN sẽ thay đổi từ mô hình phân loại sang mô hình đánh giá. Do đó xác suất được chuyển sang điểm số có tác dụng đánh giá chất lượng ảnh tạo ra thay cho xác suất. Điểm này càng lớn thì ảnh càng giống với thật và điểm này càng nhỏ thì ảnh sẽ khác với thật. Nhãn của mô hình cũng được thay đổi từ sang để phù hợp hơn với mục tiêu là chấm điểm. critic sẽ được huấn luyện nhiều lượt hơn so với generator và quá trình huấn luyện sẽ được thực hiện xen kẽ giữa critic và generator.
• Quá trình cập nhật gradient descent sẽ được thực hiện theo phương pháp RMSProp.
• Ràng buộc độ lớn weights của mô hình về một khoảng giới hạn sau mỗi mini-batch.
• Sử dụng RMSProp để cập nhật gradient descent với momentum = 0.

Ở đây đang sử dụng clipping weights sau khi update weights. Cách này làm giảm khả năng học của mô hình do giới hạn các giá trị nhận được của weights. Chúng ta có thể dùng một cách khác là gradient penalty để làm cho hàm số thỏa mãn Lipschitz continuous.

Tài liệu tham khảo

1. https://phamdinhkhanh.github.io/2020/07/25/GAN_Wasserstein.html#5-%C4%91%E1%BB%99-%C4%91o-earth-mover-em-ho%E1%BA%B7c-wasserstein
2. https://lilianweng.github.io/lil-log/2017/08/20/from-GAN-to-WGAN.html