Trong bài này chúng ta sẽ đi tính đạo hàm của hàm softmax. Đây là tiền đề để chúng ta có thể hiểu được backpropagation algorithm có liên quan đến hàm softmax.

Hàm softmax

Hàm softmax là hàm nhận vào vector n chiều các số thực và chuyển nó về vector có cùng chiều nhưng với các giá trị trong khoảng (0, 1) và tổng của chúng bằng 1.

\[s(\mathbf{x})_i = \frac{e^{x_i}}{\sum_{k=1}^{n} e^{x_k}}\]

Vector trả về thể hiện phân bố xác suất của các output trong bài toán multiclass classification.

Trong một số trường hợp giá trị ở mẫu số quá lớn có thể gây ra hiện tường tràn số. Để tránh điều này thường sẽ chia cả tử và mẫu cho một hằng số $e^{-C}$. Chúng ta sẽ có một phiên bản softmax ổn định hơn

\[\begin{align*} s(\mathbf{x})_i &= \frac{e^{x_i}}{\sum_{k=1}^{n} e^{x_k}} \\ &= \frac{e^{x_i-C}}{\sum_{k=1}^{n} e^{x_k-C}} \end{align*}\]

$C$ thường được chọn là $C = max(x_i)$.

Đạo hàm của hàm softmax

Nhớ lại công thức tính đạo hàm của phân số $f(x) = \frac{g(x)}{h(x)}$ chúng ta có $f^\prime(x) = \frac{ g\prime(x)h(x) - h\prime(x)g(x)}{h(x)^2}$.

Hàm softmax:

\[s(\mathbf{x})_i = \frac{e^{x_i}}{\sum_{k=1}^{n} e^{x_k}}\]

Đối với trường hợp $i=j$ ta có:

\[\begin{align*} \frac{\partial s_i}{\partial x_i} &= \frac{e^{x_i} \sum_{k=1}^{n} e^{x_j}- e^{x_i} e^{x_i} }{\sum_{k=1}^{n} e^{x_j} \sum_{k=1}^{n} e^{x_j} } \\ &= s_i(1-s_i) \end{align*}\]

Đối với trường hợp $i \neq j$ ta có:

\[\begin{align*} \frac{\partial s_i}{\partial x_j} &= \frac{- e^{x_i} e^{x_j} }{\sum_{k=1}^{n} e^{x_j} \sum_{k=1}^{n} e^{x_j} } \\ &= -s_{i}s_j \end{align*}\]

Khi đó ta có

\[\frac{\partial s_i}{\partial x_j} = \begin{cases} s_i(1-s_j) & if & i=j \\ -s_j.s_i & if & i \neq j \end{cases}\]

Chúng ta có Kronecker delta:

\[\delta{ij} = \begin{cases} 1 & if & i=j \\ 0 & if & i\neq j \end{cases}\]

Tổng hợp lại có đạo hàm của softmax:

\[\frac{\partial s_i}{\partial x_j} = s_i(\delta_{ij}-s_j)\]

Jacobian của hàm softmax

Hàm softmax là một hàm biến đổi vector thành vector $\mathbb{R}^n \rightarrow \mathbb{R}^n$, do đó đạo hàm riêng bậc nhất của hàm softmax được xếp thành ma trận kích thước $n \times n$ - Jacobian của hàm softmax.

\[\mathbf{J}_\mathbf{x}(\mathbf{s})= \begin{bmatrix} \frac{\partial s_1}{\partial x_1} & \frac{\partial s_1}{\partial x_2}& \dots& \frac{\partial s_1}{\partial x_n}\\ \frac{\partial s_2}{\partial x_1} & \frac{\partial s_2}{\partial x_2}& \dots& \frac{\partial s_2}{\partial x_n}\\ \dots& \dots& \dots& \dots\\ \frac{\partial s_n}{\partial x_1} & \frac{\partial s_n}{\partial x_2}& \dots& \frac{\partial s_n}{\partial x_n} \end{bmatrix}\] \[\mathbf{J}_\mathbf{x}(\mathbf{s})= \begin{bmatrix} s_1 - s_1^{2} & -s_1 s_2& \dots& -s_1 s_n\\ -s_2 s_1 & s_2 - s_2^{2}& \dots& -s_2 s_n\\ \dots& \dots& \dots& \dots\\ -s_n s_1 & s_n s_2& \dots& s_n - s_n^{2}\\ \end{bmatrix} (1)\]

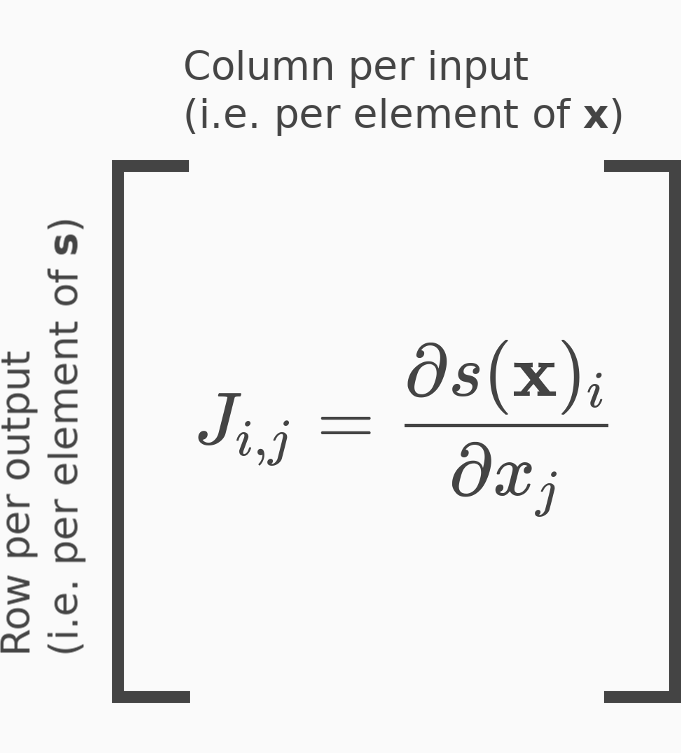
Xây dựng Jacobian matrix trong Python:

Chúng ta có thể biến đổi (1) thành:

\[\mathbf{J}_\mathbf{x}(\mathbf{s})= \begin{bmatrix} s_1 & 0 & \dots& 0\\ 0 & s_2 & \dots& 0\\ \dots& \dots& \dots& \dots\\ 0 & 0& \dots& s_n\\ \end{bmatrix} - \begin{bmatrix} s_1^{2} & s_1 s_2& \dots& s_1 s_n\\ s_2 s_1 & s_2^{2}& \dots& s_2 s_n\\ \dots& \dots& \dots& \dots\\ s_n s_1 & s_n s_2& \dots& s_n^{2}\\ \end{bmatrix}\]

Nếu chúng ta biểu diễn $\mathbf{s}$ dưới dạng vector hàng $(1, n)$ thì $\mathbf{s}^\mathit{T}$ là vetor cột $(n, 1)$. Khi đó Jacobian của softmax $\mathbf{s}$ có thể được viết lại như sau:

\[\mathbf{J}_\mathbf{x}(\mathbf{s}) = diag(\mathbf{s}) - \mathbf{s}^\mathit{T}\mathbf{s}\]

Tài liệu tham khảo

1. https://mattpetersen.github.io/softmax-with-cross-entropy
2. https://deepnotes.io/softmax-crossentropy