Eigenvectors và eigenvalues có nhiều ý nghĩa trong Conputer vision và ML. Chúng ta đã biết đến PCA (principal component analysis) cho dimensonality reduction hay Eigenfaces cho face recognition. Trong bài này chúng ta sẽ tìm hiểu về chúng cho trường hợp 2D.

Eigenvector là vector mà hướng của nó không đổi khi áp dụng linear transformation lên nó.

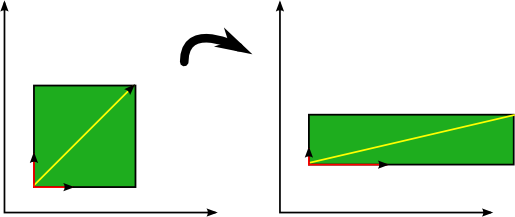
Ví dụ hình bên trên các eigenvectors (màu đỏ) không thay đổi hướng khi áp dụng liner transformation. Vector màu vàng không phải là eigenvector do nó có thay đổi hướng khi áp dụng linear transformation.

Transformation trong trường hợp này là scaling đơn giản với $s_x = 2$ theo horizontal direction và $s_y = 0.5$ theo vertical direction. Có thể biểu diễn transformation matrix hay scaling matrix như sau:

\[\mathbf{A} = \begin{bmatrix} 2& 0\\ 0& 0.5 \end{bmatrix}\]

Ban đầu có vector $\mathbf{v}$, sau khi áp dụng linear transformation chuyển thành $\mathbf{A} \mathbf{v}$. Nên nhớ chúng ta có vector cột nhé.

Nhận thấy hướng của một số vector không bị ảnh hưởng bởi linear transformation. Những vector này được gọi là eigenvectors của linear transformation đó và xác định duy nhất cho ma trân vuông $\mathbf{A}$. Tất nhiên ở đây linear transformation được xác định duy nhất bởi $\mathbf{A}$. “Eigen” còn có nghĩa là “specific” ám chỉ các vectors này xác định duy nhất cho transformation matrix $\mathbf{A}$ nào đó.

Định nghĩa và tính chất

Tổng quát, eigenvector $\mathbf{v}$ ($\mathbf{v} \neq 0$) của matrix vuông $\mathbf{A}$ là vector được xác định như sau:

\[\mathbf{A}\mathbf{v} = \lambda \mathbf{v}~~~~~(1)\]

ở đây $\lambda$ là số vô hướng, được gọi là eigenvalue tương ứng của eigenvector $\mathbf{v}$. Nhận thấy linear transformation $\mathbf{A}$ lên vector $\mathbf{v}$ được hoàn toàn xác định bởi $\lambda$.

Chú ý: Nếu ma trận vuông $\mathbf{A}$ xác định trên trường số thực $\mathbb{R}$ hay số phức $\mathbb{C}$ thì trị riêng $\lambda$ cũng xác định trên trường tương ứng.

Một số tính chất:

1. Eigenvalue $\lambda$ chính là nghiệm của phương trình $\det\left(\mathbf{A} - \lambda \mathbf{I}\right) = 0$. Đây là phương trình đặc trưng của ma trận $\mathbf{A}$. Bên dưới chúng ta sẽ suy ra điều này.

2. Một eigenvalue có thể có nhiều eigenvectors.

Nếu $\mathbf{v}$ là eigenvector ứng với eigenvalue $\lambda$ của ma trận $\mathbf{A}$ thì vector $k \mathbf{v}$ với $k \neq 0$ cũng là eigenvector của ma trận $\mathbf{A}$ tương ứng với eigenvalue $\lambda$ do

\[\mathbf{A} \left(k\mathbf{v}\right) = \lambda \left(k\mathbf{v}\right)\]

3. Mỗi eigenvector chỉ có một eigenvalue tương ứng.

Giả sử eigenvector $\mathbf{v}$ tương ứng với hai eigenvalues $\lambda_1$ và $\lambda_2$. Khi đó ta có

\[\mathbf{A} \mathbf{v} = \lambda_1 \mathbf{v}, ~~ \mathbf{A} \mathbf{v} = \lambda_2 \mathbf{v}\]

Lúc này ta có $\left( \lambda_1 - \lambda_2 \right) \mathbf{v} = 0$, do $\mathbf{v} \neq 0$ nên $\lambda_1 = \lambda_2$. Dó đó eigenvector chỉ có duy nhất một eigenvalue tương ứng.

4. Nếu $\lambda = 0$ là eigenvalue của ma trận A thì A không khả nghịch (not invertable). Ngược lại, nếu mọi eigenvalues của A đều khác không thì A khả nghịch (invertable).

Chúng ta tìm các eigenvalues từ phương trình:

\[\det \left( \mathbf{A} - \lambda \mathbf{I} \right) = 0\]

Nếu $\lambda = 0$ thì ta có $\det(\mathbf{A}) = 0$ hay ma trận A không khả nghịch.

5. Nếu $\lambda$ là eigenvalue của ma trận $\mathbf{A}$ thì $\lambda^k$ là eigenvalue của ma trận $\mathbf{A}^k$

Do $\lambda$ là eigenvalue của ma trận $\mathbf{A}$ nên ta có $\mathbf{A} \mathbf{v} = \lambda \mathbf{v}$. Nhân vào bên trái cả hai vế với $\mathbf{A}$ nhận được $\mathbf{A}^2 \mathbf{v} = \mathbf{A} \lambda \mathbf{v} = \lambda^2 \mathbf{v}$. Lúc này $\lambda^2$ là eigenvalue của ma trận $\mathbf{A}^2$. Tương tự như vậy bằng quy nạp có thể chứng minh được $\lambda^k$ là eigenvalue của ma trận $\mathbf{A}^k$.

6. Ma trận $\mathbf{A}$ là nghiệm của phương trình đặc trưng của nó (biến số bây giờ là ma trận).

Ta có đa thức đặc trưng của ma trận $\mathbf{A}$

\[P(\lambda) = \det(\mathbf{A} - \lambda \mathbf{I})\]

Lúc này

\[P(\mathbf{A}) = \det(\mathbf{A} - \mathbf{A} \mathbf{I}) = \det(\mathbf{A} - \mathbf{A}) = 0\]

Xác định eigenvalues và eigenvectors

Viết lại phương trình (1) như sau:

\[\mathbf{A} \mathbf{v} - \lambda \mathbf{v} = 0\]

hay

\[\mathbf{v} \left(\mathbf{A} - \lambda \mathbf{I}\right) = 0\]

trong đó $\mathbf{I}$ là ma trận đơn vị có cùng kích thước với $\mathbf{A}$.

Phương trình trên giống như chúng ta đi giải hệ phương trình nhiều ẩn. Nếu định thức của ma trận khác 0 thì có nghiệm duy nhất, lúc này vector $\mathbf{v} = 0$, ta không cần vector không. Do đó muốn có vector khác 0 thì định thức của ma trận bằng 0. Do đó

\[\det \left( \mathbf{A} - \lambda \mathbf{I} \right) = 0\]

Chúng ta đi làm một ví dụ sau, có ma trận $\mathbf{A}$

\[\mathbf{A} = \begin{bmatrix} 2& 3\\ 2& 1 \end{bmatrix}\]

Ta có

\[\det \begin{bmatrix} 2-\lambda& 3\\ 2& 1 - \lambda \end{bmatrix} = 0\]

Từ đây tìm được $\lambda_1 = -1$ và $\lambda_2 = 4$.

Nên nhớ ma trận vuông $n \times n$ luôn có $n$ eigenvalues, mỗi cái tương ứng với một eigenvetor.

Sau khi tìm được eigenvalue chúng ta sẽ đi xác định eigenvector tương ứng.

Đối với $\lambda_1 = -1$ ta có

\[\begin{bmatrix} 2& 3\\ 2& 1 \end{bmatrix} \begin{bmatrix} x_{11}\\ x_{12} \end{bmatrix} = -1 \begin{bmatrix} x_{11}\\ x_{12} \end{bmatrix}\] \[\left\{\begin{matrix} 2 x_{11} + 3 x_{12} = - x_{11}\\ 2 x_{11} + x_{12} = - x_{12} \end{matrix}\right.\]

Cuối cùng nhận được $x_{11} = -x_{12}$

Nhận thấy ở đây eigenvector đơn giản chỉ biểu diễn hướng, do đó chúng ta có thể nhân thêm bất kì số vô hướng khác 0 nào để nhận được eigenvectors mới song song với eigenvector đó. Nếu muốn normalize có thể normalize chúng để có norm bằng 1. Để đơn giản chọn $x_{12}=1$ và $x_{11} = -1$. Lúc này có

\[\mathbf{v}_1 = \begin{bmatrix} -1\\ 1 \end{bmatrix}\]

Tương tự đối với $\lambda_2 = 4$ chúng ta lấy

\[\mathbf{v}_1 = \begin{bmatrix} 3\\ 2 \end{bmatrix}\]

Như vậy chúng ta đã tìm hiểu về eigenvectors và eigenvalues. Các bạn có thể thực hành thêm với các ví dụ về tìm eigenvectors và eigenvalues cho ma trận vuông. Thực ra mình viết bài này để phục vụ cho bài về covariance matrix. Mọi người có thể đọc thêm tại link này.