Backpropagation với softmax và crossentropy
Trong bài trước chúng ta đã tìm hiểu về hàm softmax. Trong này chúng ta sẽ đi phân tích thuật toán backpropagation với hàm softmax và crossentropy- thuật toán được ứng dụng trong mạng Neural Network rất thành công.
Chain rule
Trước này chúng ta đã biết cách tính đạo hàm cho hàm đơn giản như:
\[\frac{\mathrm{d} x^2}{\mathrm{d} x} = 2x ~~~~~~ \frac{\mathrm{d} e^x}{\mathrm{d} x} = e^x\]Đối với các hàm phức hợp:
\[z_1 = z_1(x_1, x_2) ~~~~~~ z_2 = z_2(x_1, x_2) ~~~~~~ p = p(z_1, z_2)\]trong đó $z_1, z_2$ khả vi. Khi đó chain rule có thể được hiểu như sau:
\[\frac{\partial p}{\partial x} = \frac{\partial p}{\partial z_1} \frac{\partial z_1}{\partial x} + \frac{\partial p}{\partial z_2} \frac{\partial z_2}{\partial x}\]Tổng quát: nếu có hai hàm $f(x)$ và $g(x) $ khả vi
- $h(x) = (f \circ g)(x)$ cũng khả vi:
- $y = f(u)$ và $u = g(x)$ khi đó:
Ví dụ $h(x) = f(x) ~ g(x)$ ta có:
\[\frac{\partial h}{\partial x} = \frac{\partial h}{\partial f} \frac{\partial f}{\partial x} + \frac{\partial h}{\partial g} \frac{\partial g}{\partial x}\]Cross entropy
Trong bài toán multiclass classification chúng ta có giá trị thực tế $y_i$, giá trị dự đoán $\hat{y}_i$ (đầu ra hàm softmax). Khi đó cross entropy loss được xác định như sau.
\[L = - \sum_i y_i log(\hat{y}_i)\] \[\hat{y}(\mathbf{z})_i = \frac{e^{z_i}}{\sum_{k=1}^{n} e^{z_k}}\]Đi xác định đạo hàm của loss theo các predicted nodes (units).
\[\begin{align} \frac{\partial L}{\partial z_i} &= - \sum_k y_k \frac{\partial log(\hat{y}_k)}{\partial z_i} \\ &= - \sum_k y_k \frac{\partial log(\hat{y}_k)}{\partial \hat{y}_k} \times \frac{\partial \hat{y}_k}{ \partial z_i} \\ &= - \sum_k y_k \frac{1}{\hat{y}_k} \times \frac{\partial \hat{y}_k}{\partial z_i} \\ \end{align}\]Nhớ lại bài trước, đạo hàm của softmax theo từng thành phần
\[\frac{\partial \hat{y}_k}{\partial z_i} = \hat{y}_k(\delta_{ki} - \hat{y}_i)\]với
\[\delta_{ki} = \begin{cases} 1 & if & k=i \\ 0 & if & k \neq i \end{cases}\]Do đó (3) tương đương với:
\[\begin{align*} \frac{\partial L}{\partial z_i} &= - \sum_k y_k \frac{1}{\hat{y}_k} \times \hat{y}_k(\delta_{ki} - \hat{y}_i) \\ &= - y_i \frac{1}{\hat{y}_i} \times \hat{y}_i(1 - \hat{y}_i)- \sum_{k \neq i} y_k \frac{1}{\hat{y}_k} \times \hat{y}_k(- \hat{y}_i) \\ &= - y_i (1-\hat{y}_i) + \sum_{k \neq i} y_k \hat{y}_i \\ &= - y_i + y_i \hat{y}_i + \sum_{k \neq i} y_k \hat{y}_i \\ &= - y_i + \hat{y}_i (y_i + \sum_{k \neq i} y_k) \end{align*}\]Do tổng các phần tử của softmax bằng 1 hay $\sum_k y_k = y_i + \sum_{k \neq i} y_k = 1$ nên chúng ta có:
\[\frac{\partial L}{\partial z_i} = \hat{y}_i -y_i ~~~~ (4)\]Kí hiệu $w_{pq}$ là weight kết nối units thứ $p$ của layer trước với unit thứ $q$ của output layer, $a_p$ là giá trị đầu ra của unit thứ p của layer trước, chúng ta có:
\[z_k=\sum_iw_{ik}a_i+b_k \implies \frac{\partial z_k}{\partial w_{pq}}=\sum_i a_i\frac{\partial w_{ik}}{\partial w_{pq}}=\sum_i a_i\delta_{ip}\delta_{kq}=\delta_{kq} a_p ~~~~ (5)\]Có biểu thức cuối do $i$ theo chạy theo số units của layer trước và $\delta_{ip} = 1 $ khi $i=p$.
Chốt lại từ (4) và (5) chúng ta có:
\[\frac{\partial L}{\partial w_{pq}} = \sum_k\frac{\partial L}{\partial z_k}\frac{\partial z_k}{\partial w_{pq}} = \sum_k(\hat{y}_k - y_k)\delta_{kq} a_p = a_p(\hat{y}_q - y_q)\]hay
\[\frac{\partial L}{\partial w_{ij}} = a_i(\hat{y}_j - y_j)\]Như vậy chúng ta đã làm từng bước tính đạo hàm của loss so với weights cho output layer. Một cách tổng quát hơn.
\[\frac{\partial L}{\partial w_{pq}}=\sum_i \frac{\partial L}{\partial \hat{y}_i}\frac{\partial \hat{y}_i}{\partial w_{pq}}\] \[\frac{\partial \hat{y}_i}{\partial w_{pq}} = \sum_k \frac{\partial \hat{y}_i}{\partial z_k}\frac{\partial z_k}{\partial w_{pq}}\]Kết hợp lại sẽ có:
\[\frac{\partial L}{\partial w_{pq}}=\sum_i \left[ \frac{\partial L}{\partial \hat{y}_i}\left(\sum_k \frac{\partial \hat{y}_i}{\partial z_k}\frac{\partial z_k}{\partial w_{pq}}\right) \right]\]trong đó $i, k$ đều chạy trong số units của output layer.
Đi vào một ví dụ cụ thể xem thế nào.
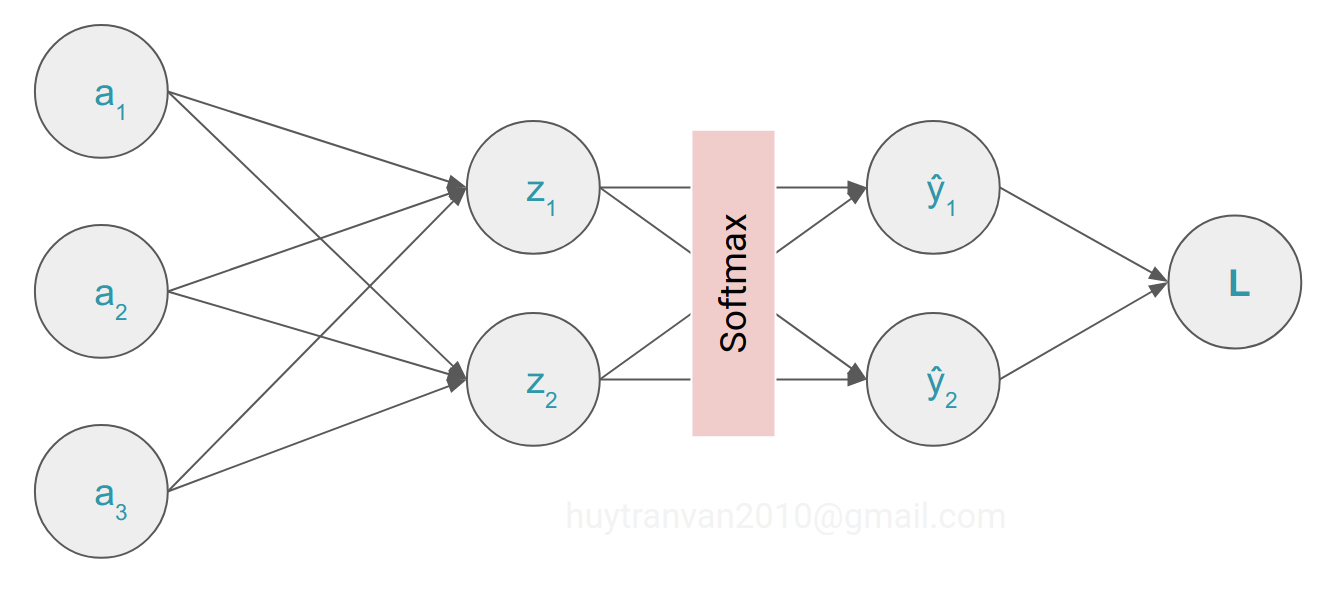
Chúng ta sẽ đi tính đạo hàm của loss theo $w_{21}$ và $b_1$. Chúng ta đánh dấu đường đi (liên quan) cho dễ hiểu.
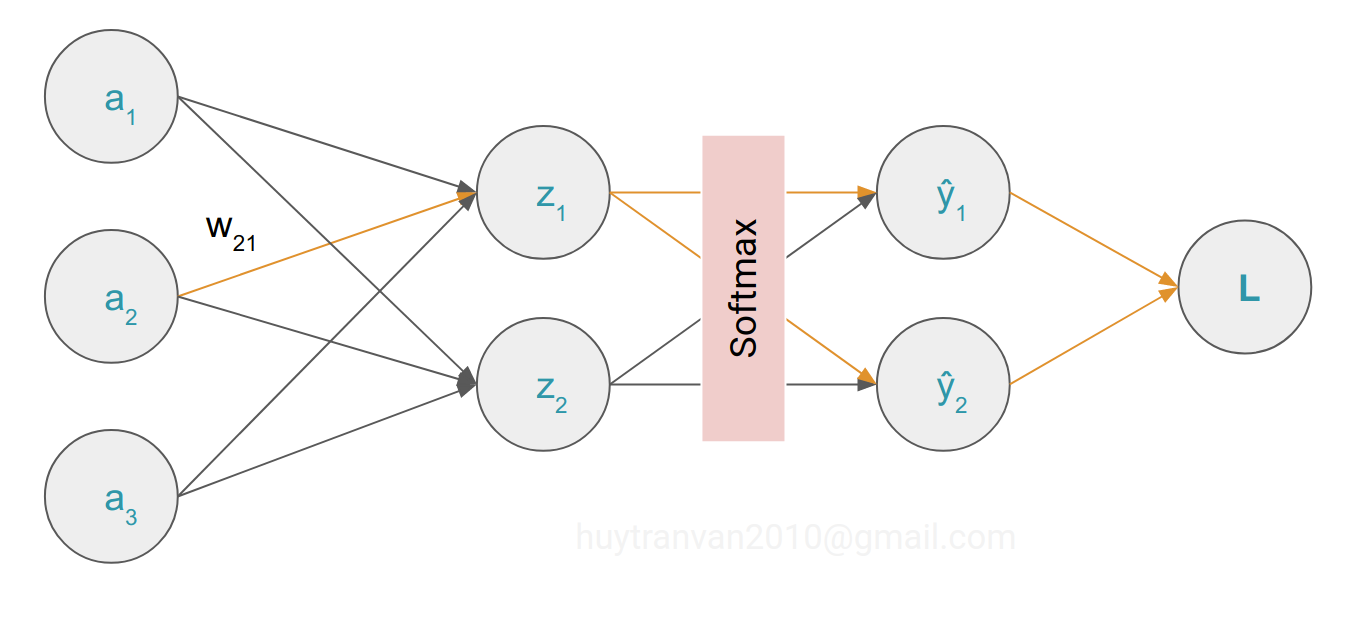
Cuối cùng áp dụng chain rule cho $w_{21}$ ta có:
\[\begin{align*} \frac{\partial L}{\partial w_{21}} &= \frac{\partial L}{\partial \hat{y}_1}\frac{\partial \hat{y}_1}{\partial z_1}\frac{\partial z_1}{\partial w_{21}} + \frac{\partial L}{\partial \hat{y}_2}\frac{\partial \hat{y}_2}{\partial z_1}\frac{\partial z_1}{\partial w_{21}}\\ &= \frac{-y_1}{\hat{y}_1}[\hat{y}_1(1 - \hat{y}_1)] a_2 + \frac{-y_2}{\hat{y}_2}(-\hat{y}_2 \hat{y}_1) a_2\\ &= a_2(- y_1 + y_1 \hat{y}_1 + y_2 \hat{y}_1 )\\ &= a_2(\hat{y}_1(y_1 + y_2) - y_1)\\ &= a_2(\hat{y}_1 - y_1) \end{align*}\]Đối với $b_1$ ta có:
\[\begin{align*} \frac{\partial L}{\partial b_1} &= \frac{\partial L}{\partial \hat{y}_1}\frac{\partial \hat{y}_1}{\partial z_1}\frac{\partial z_1}{\partial b_1} + \frac{\partial L}{\partial \hat{y}_2}\frac{\partial \hat{y}_2}{\partial z_1}\frac{\partial z_1}{\partial b_1}\\ &= \frac{-y_1}{\hat{y}_1}[\hat{y}_1(1 - \hat{y}_1)] + \frac{-y_2}{\hat{y}_2}(-\hat{y}_2 \hat{y}_1) \\ &= - y_1 + y_1 \hat{y}_1 + y_2 \hat{y}_1 \\ &= \hat{y}_1(y_1 + y_2) - y_1 \\ &= \hat{y}_1 - y_1 \end{align*}\]Như vậy chúng ta đã cùng tìm hiểu backpropagation algorithm cho hệ số của output layer. Hy vọng các bạn tìm thấy điều gì hữu ích từ bài viết.
Tài liệu tham khảo
- https://peterroelants.github.io/posts/neural-network-implementation-part02/
- https://stats.stackexchange.com/questions/235528/backpropagation-with-softmax-cross-entropy
- https://en.wikipedia.org/wiki/Chain_rule#Higher_dimensions
- https://eli.thegreenplace.net/2016/the-softmax-function-and-its-derivative/