mAP - mean Average Precision for Object Detection
mAP (mean average precision) là độ đo phổ biến để đánh giá độ chính xác của bài toán object detection như Faster R-CNN, SSD… mAP chính là trung bình của các average precision của từng class. Trước khi tìm hiểu về mAP chúng ta cùng nhắc lại một số khái niệm như precision, recall trong bài toán phân loại.
Ví dụ bài toán phân loại phụ nữ có thai hay không thì việc có thai coi là Positive, việc không có thai coi là Negative. True/False thể hiện sự dự đoán đúng hay sai.
- True Positive: dự đoán có thai - Positive, thực tế thì có thai (True)
- False Positive: dự đoán có thai - Positive, thực tế thì không có thai (False). Dự đoán người không có thai thành có thai.
- True Negative: dự đoán không có thai - Negative, thực tế không có thai (True)
- False Negative: dự đoán không có thai - Negative, thực tế thì có thai (False)

Precision và Recall
\[\text{Precision} = \frac{TP}{TP+FP}\] \[\text{Recall} = \frac{TP}{TP+FN}\] \[\frac{2}{F1} = \frac{1}{\text{Precision}} + \frac{1}{\text{Recall}}\]trong đó: $TP$ - True Positive, $TN$ - True Negative, $FP$ - False Positive, $FN$ - False Negative.
IoU - Intersection over union
IoU (còn có tên khác là Jaccard index) là giá trị đo độ chồng chập giữa 2 bounding boxes. Chúng ta thường dùng IoU để đo độ khớp của predicted box và ground-truth box. Đối với bài toán object detection chúng ta hay dùng IoU để xác định precision và recall.
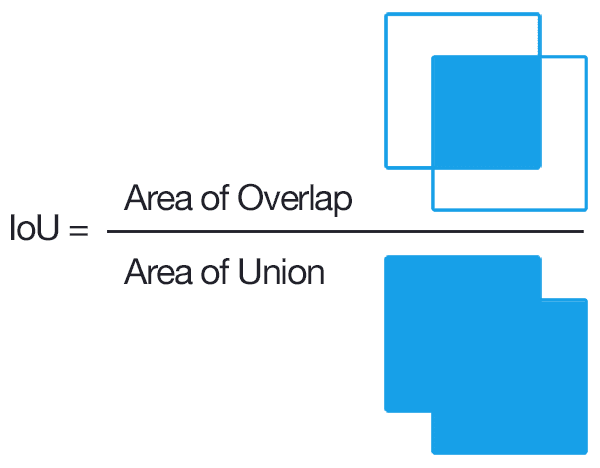
Đối với bài toán object detection:
- TP (True Positive): là các predicted box với IoU ≥ threshold. TP hiểu là dự đoán đúng, thành positive, trong TH này dự đoán đúng là các predicted box với IoU > threshold, positive nghĩa là có object
- FP (False Positive): là các predicted box với IoU < threshold. FP hiểu là dự đoán sai thành positve, trong TH này dự đoán sai là predicted box với IoU < threshold. Ở đây ám chỉ có dự đoán ra được bounding box
- FN (False Negative): mô hình không dự đoán được đối tượng trong ảnh đối với ground truth box hay groudth-truth box không được gắn với predicted bounding box nào
- TN (True Negative): không được dùng. Đây là những phần của ảnh không chứa đối tượng (không được gán ground-truth box) và được dự đoán không chứa đối tượng (thực chất mô hình chỉ đưa ra các vùng có khả năng chứa đối tượng). Điều này có nghĩa rằng các vùng khác trong ảnh được dự đoán là không chứa đối tượng. Số lượng TN như vậy là vô số.
Ví dụ như hình dưới nếu IoU threshold là 0.5, IoU cho dự đoán là 0.7 khi đó chúng ta có TP - dự đoán đúng. Ngược lại nếu IoU là 0.3, chúng ta có FP - dự đoán sai. Tạm thời chưa quan tâm đến confidence score.
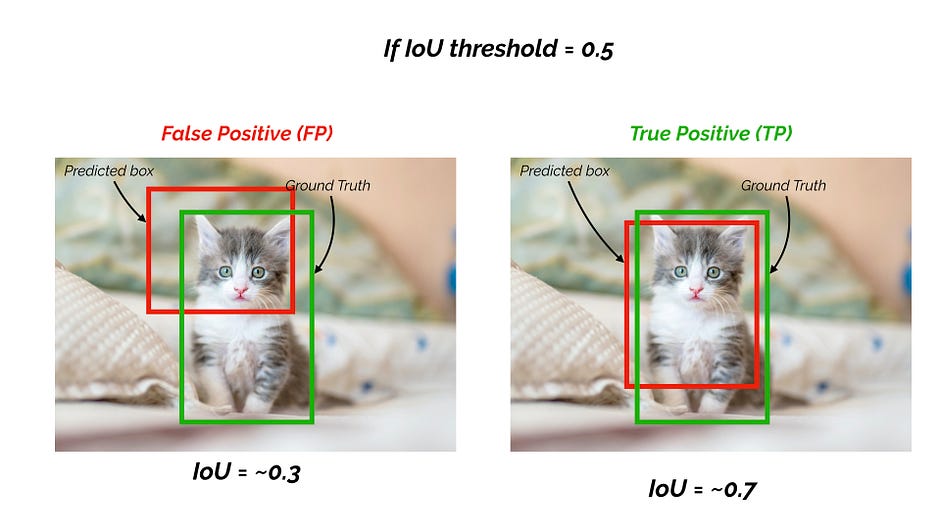
Predicted boxes phải được phân loại vào đúng class trước và sau đó chúng ta mới đi xác định precision và recall dựa trên IoU. Phân loại sai class mà xác định IoU thì không có ý nghĩa.
Và khi chúng ta thay đổi IoU threshold, False Positive có thể chuyển thành True Positive như hình dưới đây.
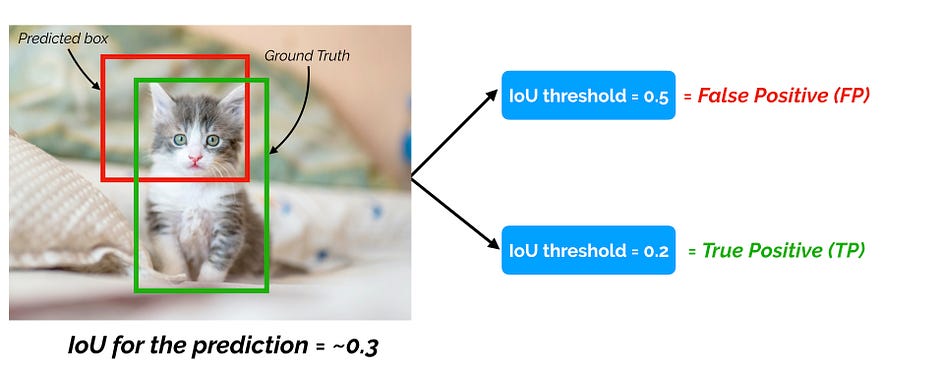
Precision là tỉ lệ các dự đoán đúng (khớp với ground truth boxes) so với tổng số các dự đoán (predicted bounding boxes) do đó:
\[\text{Precision} = \frac{\text{true object detection}}{\text{all predicted boxes}} = \frac{TP}{TP + FP}\]Recall (độ nhạy) thể hiện tỉ lệ dự đoán đúng trên tổng số ground truth.
\[\text{Recall} = \frac{\text{true object detection}}{\text{all ground truth boxes}} = \frac{TP}{\text{\# ground truth boxes}}\]Nhận thấy một model tốt phải có cả precision và recall cao. Bạn đọc có thể tự suy luận từ hai công thức trên. Chúng ta cũng chỉ cần biết TP, FP và số lượng ground truth boxes là có thể xác định được precision và recall.
AP - average precision
Average Precision (AP) is the area under the precision-recall curve - diện tích nằm dưới đường precision-recall.
Precision-recall curve là đường thể hiện mối quan hệ của precision so với recall khi thay đổi ngưỡng confidence score.

Thông thường khi tăng threshold thì precision sẽ tăng và recall sẽ giảm.
Chúng ta sẽ tính AP (average precision) thông qua một ví dụ dưới đây. Trong tập dữ liệu chỉ chứa 5 quả táo. Chúng ta thu thập tất cả các dự đoán cho tất cả các hình ảnh và xếp hạng theo thứ tự giảm dần của confidence score tương ứng với mỗi predicted bounding box. Cột thứ hai thể hiện dự đoán đúng hay không. Trong ví dụ này dự đoán được coi là đúng nếu có $IoU \geq 0.5$

Cùng xem dòng rank#3, precision và recall được tính như nào mà có kết quả như vậy:
- Precision = 2/3 = 0.67 (dự đoán đúng được 2 quả táo TP và dự đoán một quả khác thành quả táo FP)
- Recall = 2/5 = 0.4 (do có tổng cộng 5 quả táo $TP + FN = \text{all ground-truth boxes}$ và dự đoán đúng được 2 quả táo TP)
Nhận thấy giá trị của recall không giảm khi chúng ta đi xuống theo chiều giảm confidence score tuy nhiên precision lại đi theo đường zigzag (có thể tăng lên nhưng xu hướng chung là giảm).
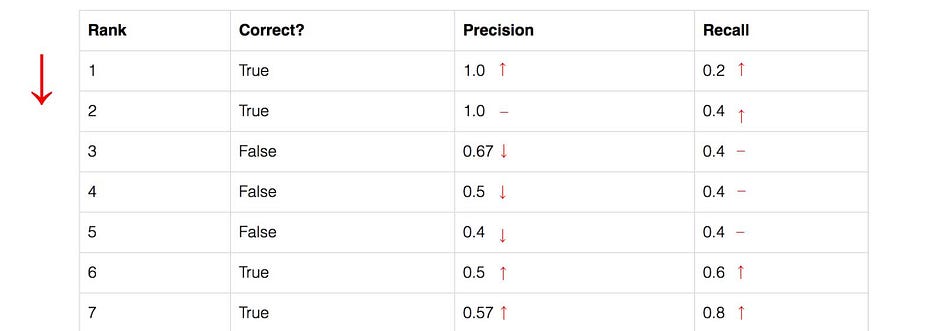
Vẽ sự phụ thuộc của precision và giá trị của recall (lấy từ bảng trên cùng).
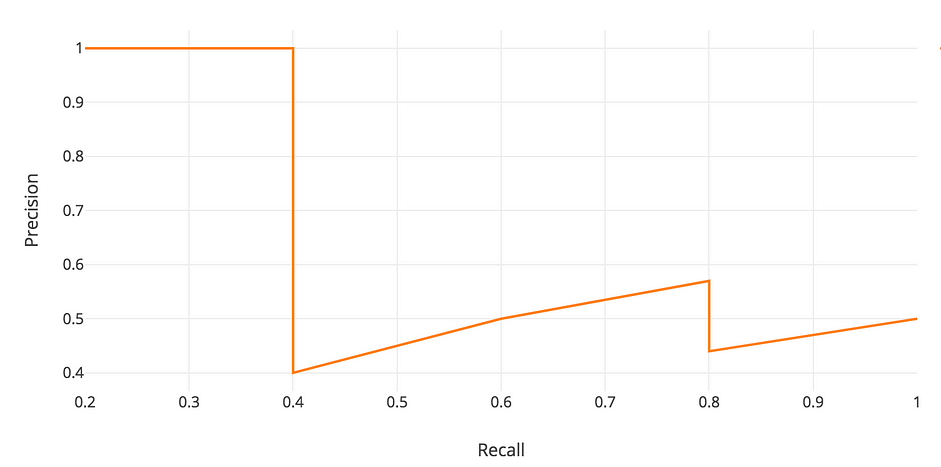
Precision-recall curve
Định nghĩa chung của Average Precision (AP) là area under the precision-recall curve (diện tích dưới đường precision-recall):
\[AP = \int_{0}^{1} P(r) dr\]trong đó $P(r)$ thể hiện sự phụ thuộc của precision vào recall.
Giá trị của precision và recall luôn nằm trong [0, 1] do đó AP cũng nằm trong [0, 1]. Trước khi tính AP cho bài toán object detection người ta người làm trơn đường zigzag trước (loại bỏ một số điểm precision tăng khi confidence giảm).
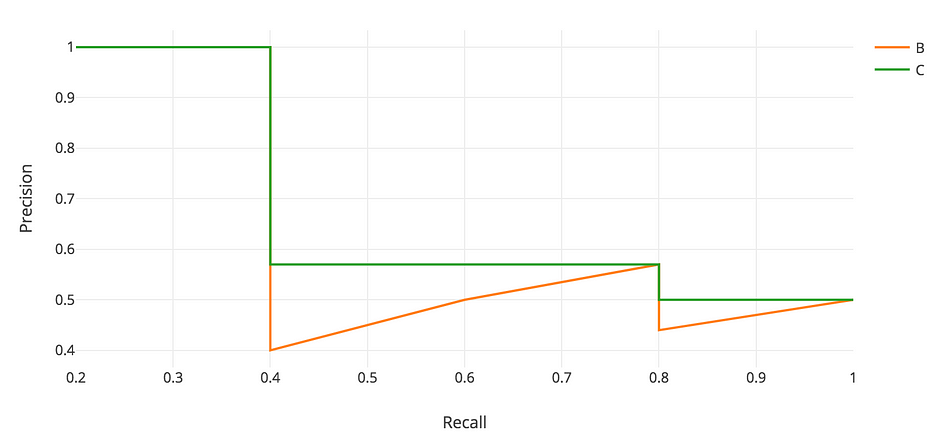
Nhìn trên hình nhận thấy tại mỗi mức recall chúng ta sẽ thay thế precision bằng giá trị max precision ở bên phải mức recall đó (ví dụ recall trong [0.4, 0.8] sẽ lấy precision max là 0.57 tại recall = 0.8 do nó nằm bên phải, recall trong [0.8, 1] sẽ lấy precision max là 0.5 do nó nằm bên phải). Đến đây chắc cũng đã dễ hiểu hơn.
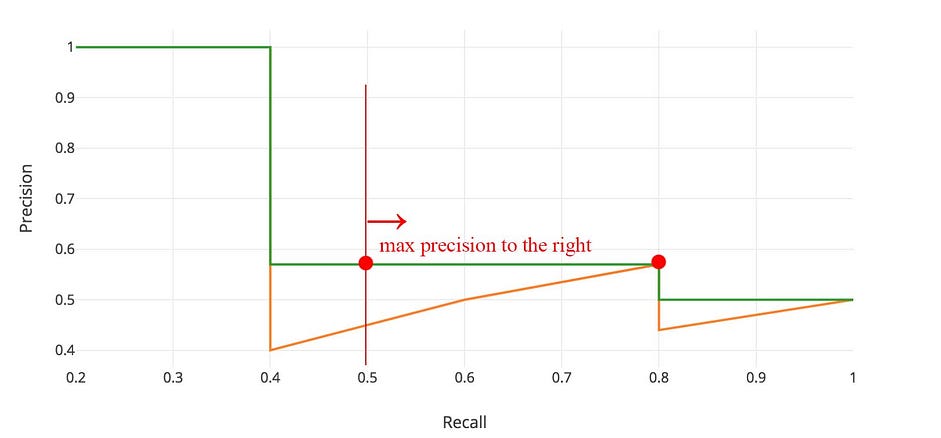
Như vậy đường màu cam sẽ chuyển thành đường màu xanh. Giá trị AP tính được sẽ ít bị ảnh hưởng bởi các thay đổi nhỏ. Tổng quát ta có thể ghi lại
\[P_{interp}(r) = \underset{\tilde{r} \geq r} {\text{max} ~ P(\tilde{r})}\]Cùng xem một ví dụ sau để hiểu hơn về interpolated average precision.

Ví dụ trên có 7 bức ảnh với 15 ground truth bounding boxes (màu xanh lá) và 24 predicted bounding boxes (màu đỏ). Các số bên cạnh các chữ cái (A-Z) biểu thị confidence score level của mô hình cho các predicted boxes đó.
Bảng sau thể hiện các bounding boxes với các confidences tương ứng. Cột cuối cùng chỉ ra detection là TP hoặc FP (như đã nói ở trên predicted boxes liên quan đến TP hoặc FP). Trong ví dụ này TP khi có $IoU \ge 0.3$ (IoU của predicted box và ground truth box), ngược lại thì predicted box $IoU < 0.3$ thì được coi là FP. Nhìn vào các hình trên gần đúng có thể thấy detection là TP hay FP dựa vào IoU.

Nhận thấy trong các ảnh 2, 3, 4, 5, 6, 7 một số ground truth bbox bị overlap với nhiều predicted bbox thì predicted bbox có IoU cao nhất sẽ được coi là True Positive (TP), các predicted bbox còn lại sẽ được coi là FP (False Positive). Ví dụ với image2, 2 predicted box D, E đều có $IoU \ge 0.3$ nhưng box E có IoU cao hơn nên được coi là TP, D được xem là FP.
Precision recall curve thể hiện mối liên hệ giữa Precision và Recall tích lũy khi điều chỉnh ngưỡng confidence score. Đầu tiên chúng ta cần sắp xếp các detections theo chiều giảm của confidence score, sau đó tính precision và recall cho accumulated detection. Chúng ta có AccTP - TP tích lũy và AccFP - FP tích lũy, AccTP và AccFP sẽ được cộng dồn từ TP / FP theo chiều tăng của confidence score.
Chú ý: Đối với việc tính recall, do mẫu số AccTP + Acc FN chính là tổng số ground truth bounding boxes ban đầu.
Từ bảng phía trên kết hợp với lập luận vừa rồi chúng ta có bảng tổng kết như sau:

Bảng trên được sắp xếp theo chiều giảm dần của confidence score, IoU của các predicted box đã được xác định và xác định nó là TP hay FP. Thông số của bảng trên được diễn giải như sau:
>>> Row 1 - image5 - predicted box R - confidence score = 0.95
- R có IoU cao hơn so với S nên R là TP, AccTP = 1, AccFP = 0
- Precision = 1 / (1 + 0) = 1
- Recall = 1 / (all ground truths) = 1 / 15 = 0.0666
>>> Row 2 - image7 - predicted box Y - confidence score = 0.95
- Y có conf score cao nhưng IoU < 0.3 nên Y là FP, AccTP vẫn = 1, AccFP = 1
- Precision = 1 / (1 + 1) = 0.5
- Recall = 1 / (all ground truths) = 1 / 15 = 0.0666
>>> Row 3 - image3 - predicted box J - conf score = 0.91
- J có IoU > 0.3 nên J là TP. Do đó AccTP = 1 + 1 = 2, AccFP = 1
- Precision = 2 / (2 + 1) = 2 / 3 = 0.666
- Recall = 2 / (all ground truths) = 2 / 15 = 0.1333
...
>>> Row 24
- O có IoU = 0 < 0.3 nên O là FP ==> AccTP = 7, AccFP = 16 + 1 = 17
- Precision = 7 / (7 + 17) = 7 / 24 = 0.2917
- Recall = 7 / 15 = 0.46666
Từ bảng trên chúng ta sẽ vẽ được Precision - Recall curve

11-Interpolated AP
PASCAL VOC là bộ dataset phổ biến cho object detection. Trước VOC Challenge 2010 dùng mAP được tính dựa trên 11-interpolateded AP. Dự đoán được coi là positive nếu $IoU \geq 0.5$. Nếu multiple detections của cùng object được phát hiện, nó chỉ tính một cái, các cái còn lại được coi là negative.
Chú ý: Ở đây đang nói tới giai đoạn sau cùng, sau khi thực hiện inference, NMS rồi còn lại bao nhiêu bounding boxes chúng ta sẽ đi so sánh với groud-truth boxes để xác định positive, negative.
Trong PASCAL VOC 2008, trung bình của 11 điểm interpolated AP được xác định.

Trong ví dụ này $AP = (1 + 0.666 + 0.4285 \times 3 + 0 \times 6)/11 = 26.84$
Một ví dụ khác:
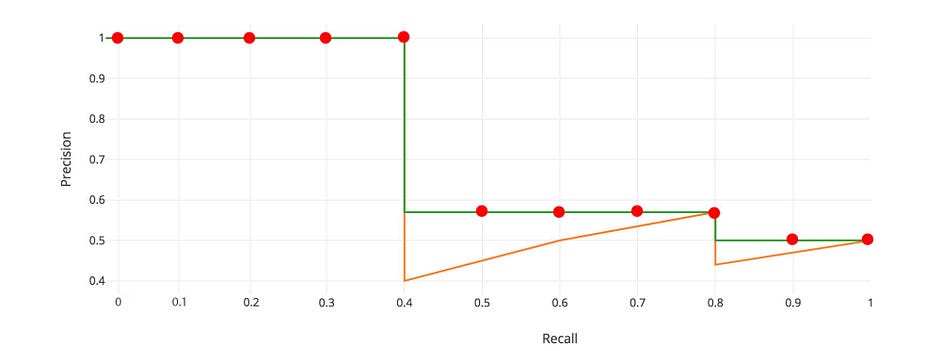
Trong ví dụ này $AP = (5 \times 1.0 + 4 \times 0.57 + 2 \times 0.5)/11 = 0.75$
Đầu tiên chúng ta chia các giá trị recall trong [0, 1] thành 11 điểm: 0, 0.1, …, 0.9, 1.0. Sau đó chúng ta tính trung bình của các interpolated precisions cho 11 giá trị recall đó.
\[AP = \frac{1}{11} (AP_r(0) + AP_r(0.1)+...+AP_r(1.0))\]Công thức tổng quát ở đây:
\[AP = \frac{1}{11} \sum_{r\in 0, 0.1, ... ,1.0} AP_r = \frac{1}{11} \sum_{r\in 0, 0.1, ... ,1.0} P_{interp}(r)\]trong đó giá trị nội suy của precision cho recall được xác định như sau:
\[P_{interp}(r) = \underset{\tilde{r} \geq r} {\text{max} ~ P(\tilde{r})}\]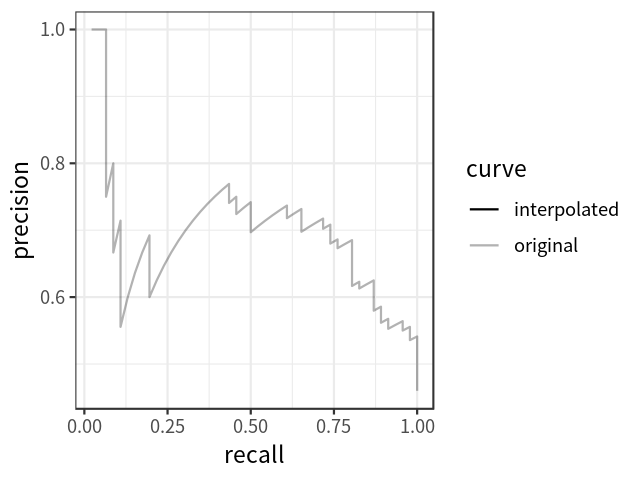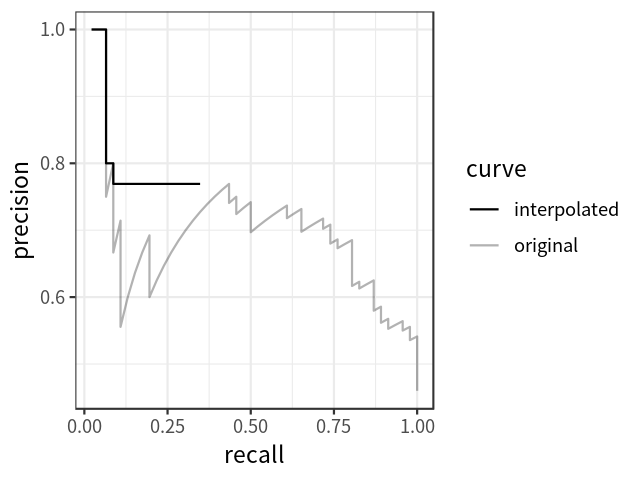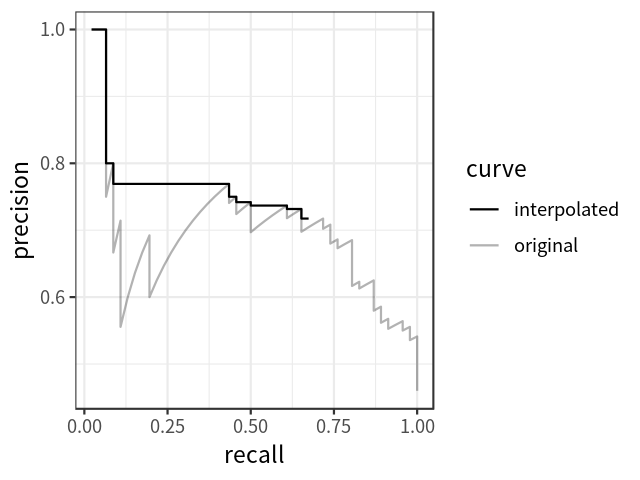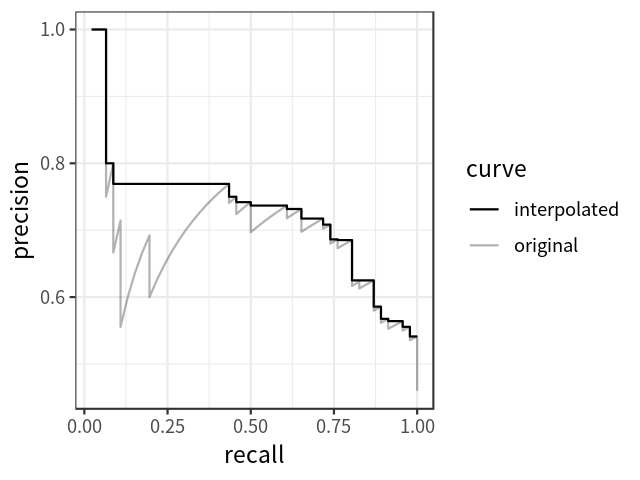
Đối với 20 classes trong PASCAL VOC chúng ta sẽ tính $AP$ cho từng class. Interpolated method (phương pháp nội suy) này là phương pháp tính gần đúng tuy nhiên nó gặp một số vấn đề. Đầu tiên nó ít chính xác, thứ hai nó mất khả năng đo lường sự khác nhau giữa các phương pháp mà AP thấp. Do đó cần một cách tính AP khác được áp dụng sau năm 2008 cho PASCAL VOC.
All-point interpolated AP
Đối với PASCAL VOC 2010-2012 chúng ta sẽ lấy các giá trị recall $r_1, r_2…$ bất cứ khi nào maximum precision bị giảm xuống. Với sự thay đổi này chúng ta đo được chính xác diện tích dưới precision-area curve sau khi loại bỏ đường zigzag.
Thay vì lấy 11 điểm, chúng ta sẽ lấy $p(r_i)$ mỗi khi nó giảm xuống và tính $AP$ như tổng diện tích của tất cả các blocks hình chữ nhật:
\[AP = \sum (r_{n+1}-r_n) ~ P_{interp}(r_{n+1})\] \[P_{interp}(r) = \underset{\tilde{r} \geq r} {\text{max} ~ P(\tilde{r})}\]Định nghĩa này được gọi là Area Under Curve (AUC).
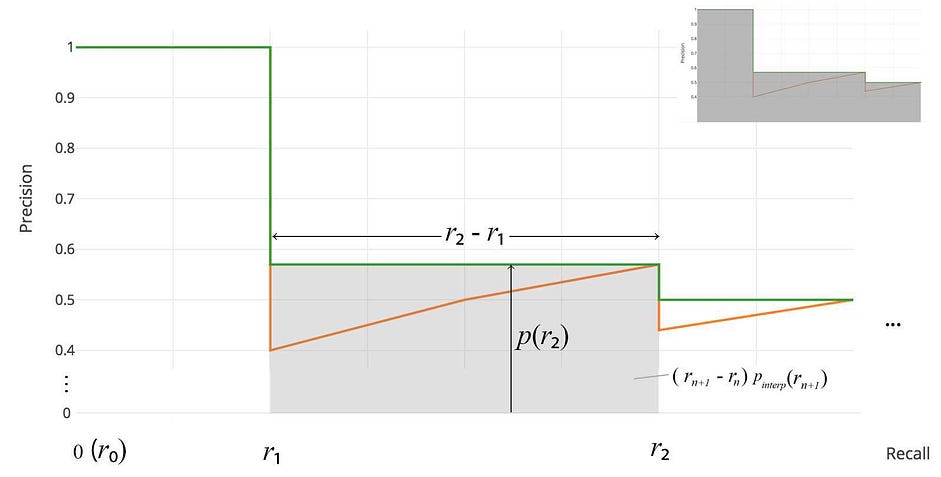
Cùng nhìn vào ví dụ chúng ta đã xét ở trên

Chúng ta sẽ đi từ phải qua trái tương ứng với recall giảm dần. Mỗi khi recall giảm chúng ta sẽ lấy precision bằng với giá trị cao nhất (phía bên phải của nó).

Sau khi tính tổng các diện tích, chúng ta có AP:
\[AP = A1 + A2 + A3 + A4\]với
- $A1 = (0.0666-0) \times 1 = 0.0666$
- $A2 = (0.1333-0.0666) \times 0.6666 = 0.0444$
- $A3 = (0.4-0.1333) \times 0.4285 = 0.1143$
- $A4 = (0.4666-0.4) \times 0.3043 = 0.0202$
do đó $AP = 0.0666 + 0.0444 + 0.1143 + 0.0202 = 0.2455 = 24.55 \%$
Nhận thấy kết quả của 2 interpolation methods có sự chênh lệch ít: $24.5 \%$ và $26.84 \%$. Phần này các bạn có thể xem thêm tại đây.
COCO mAP
Các nghiên cứu mới nhất hay đưa ra kết quả trên mỗi tập dữ liệu COCO. Trong COCO mAP interpolated AP cho 100 điểm được tính. Đối với COCO, AP là trung bình trên nhiều IoU (IoU nhỏ nhất được coi là positive). AP@[.5:.95] tương ứng với average AP cho $IoU$ từ 0.5 đến 0.95 với step là 0.05. Trong các cuộc thi COCO, AP là trung bình của 10 $IoU$ trên 80 categories. Dưới đây là một số metrics cho COCO dataset:
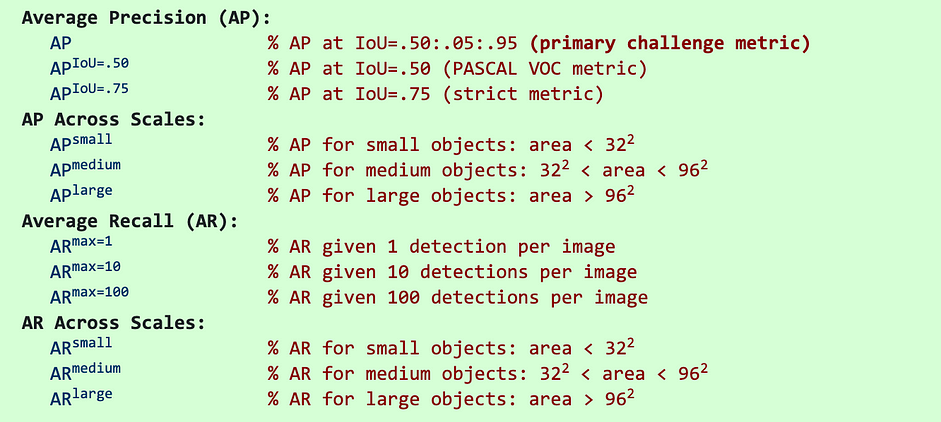
Kí hiệu $AP^{small/medium/large}$: AP cho small/medium/large object (object có kích thước: nhỏ hơn 32×32; từ 32×32 đến 96×96; lớn hơn 96×96).
Dưới đây là kết quả AP cho YOLOv3:
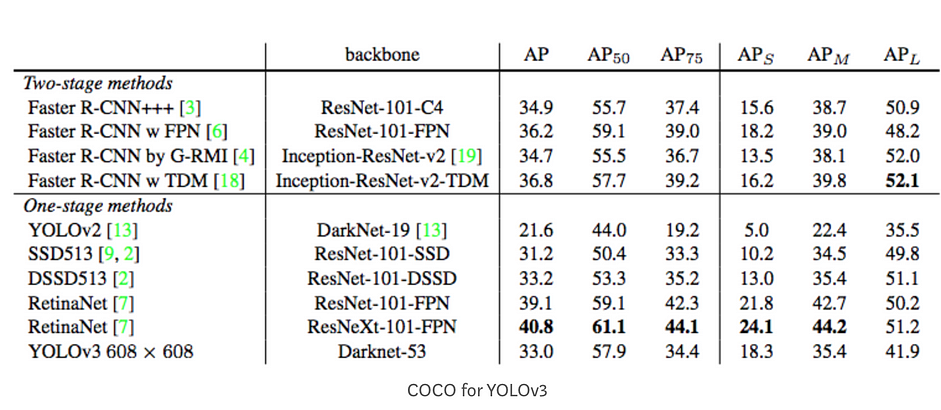
Trong hình trên $AP_{75}$ tương với với AP với $IoU=0.75$.
mAP (mean average precision) là trung bình của AP. Trong một số trường hợp chúng ta tính AP cho mỗi class và lấy trung bình. Nhưng trong một số trường hợp khác AP và mAP lại giống nhau.
AP is averaged over all categories. Traditionally, this is called “mean average precision” (mAP). We make no distinction between AP and mAP (and likewise AR and mAR) and assume the difference is clear from context
mAP được tính bằng cách lấy trung bình AP trên tất cả các class và/hoặc trên tất cả IoU threshold (phụ thuộc vào từng hoàn cảnh).
\(mAP = \frac{1}{n}\sum_{k=1}^n AP_{k}\) trong đó:
- $AP_k$ là average precision cho class $k$
- $n$ là tổng số classes.
Trong PASCAL VOC2007 challenge, AP cho một class được tính cho một IoU threshold. Do đó mAP là trung bình của AP trên toàn bộ các classes (duy nhất 1 IoU threshold).
Trong COCO 2017 challenge, mAP là trung bình trên toàn bộ các clasess và 10 IoU thresholds.
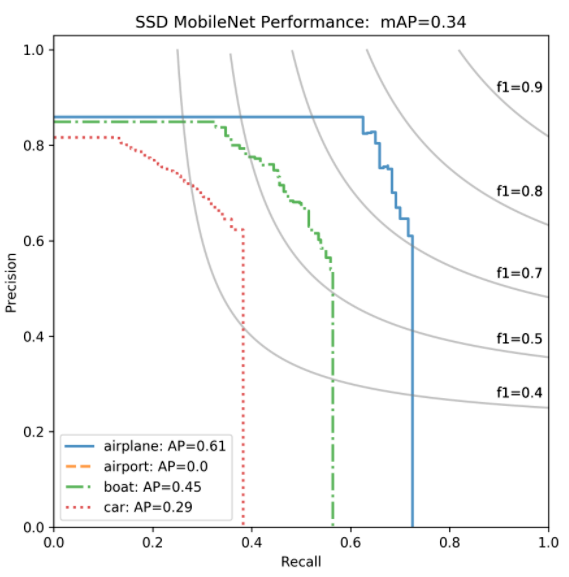
Precision-recall curve for SSD model for 4 object classes, where IoU threshold is 0.5. Van Etten, A. (2019, January)
Có một repo rất hay giúp chúng ta tính mAP cho các bài toán object detection, các bạn xem ở đây.
Tài liệu tham khảo
- https://github.com/rafaelpadilla/Object-Detection-Metrics
- https://jonathan-hui.medium.com/map-mean-average-precision-for-object-detection-45c121a31173
- https://scikit-learn.org/stable/modules/generated/sklearn.metrics.average_precision_score.html
- https://towardsdatascience.com/map-mean-average-precision-might-confuse-you-5956f1bfa9e2#:~:text=mAP%20(mean%20average%20precision)%20is,averaged%20to%20get%20the%20mAP.&text=The%20mean%20Average%20Precision%20or,different%20detection%20challenges%20that%20exist.
- https://pro.arcgis.com/en/pro-app/2.7/tool-reference/image-analyst/how-compute-accuracy-for-object-detection-works.htm#:~:text=In%20object%20detection%20and%20classification,can%20be%20true%20or%20false.&text=True%20positive—The%20model%20predicted,tree%2C%20and%20it%20is%20incorrect.
- https://towardsdatascience.com/breaking-down-mean-average-precision-map-ae462f623a52
- https://www.kdnuggets.com/2021/03/evaluating-object-detection-models-using-mean-average-precision.html
- https://www.youtube.com/playlist?list=PL1GQaVhO4f_jE5pnXU_Q4MSrIQx4wpFLM
- https://manalelaidouni.github.io/Evaluating-Object-Detection-Models-Guide-to-Performance-Metrics.html